qwen3-next线性注意力公式推导

gogongxt2025-11-212025-12-24

传统Attention Soft注意力计算复杂度（以双向注意力也就是忽略mask来着）

先来看注意力计算机制：

其中是点乘，表示mask

为了方便展示，我们先忽略 softmax 符号和（可吸收到矩阵中去）：

1、先计算

2、先计算

先计算时，复杂度为

在长序列场景下，，所以先计算的复杂度是要远远低于先计算的

但是，由于softmax的限制，没办法进行交换运算，导致长序列场景下计算复杂度很高。

那么，能不能不使用softmax计算注意力呢？

对于双向注意力来说，由于没有矩阵，可以直接交换矩阵相乘的顺序来达到降低复杂度的目的，但是对于单向注意力来说，由于的存在，不满足矩阵交换相乘，不能直接进行交换。

把写成分量的形式：

其中，为当前的分量，和为历史和的分量转换成如下形式：

$令$

则

可见，如上形式可以看成是一个以为State的线性RNN。

是历史和的外积之和，存储了所有的历史信息，我们只需要维护一个固定大小的状态矩阵而无需燰存所有历史对。

这样的好处是在长序列场景下，无需额外的显存来存储对（序列越长需要的显存越高），只需固定大小的显存来存储状态矩阵，空间复杂度从到

不过，固定大小的状态矩阵是无法完美的存储所有历史信息的，每当新加入token的时俣，现有token就要被压缩，当序列长度变得很长的时候，每个token的信息占比很小，这就是为什么线性注意力检索能力比较差。

那么，一个很直观的想法是加入新token的时候遗忘掉一些不重要的历史信息（除旧迎新）。

可以给历史状态加入一个decay因子：

可以是在一个 0 到 1 之间的常数（静态囊减因子）也可以是与输入相关的（data－dependent decay）：

我们使用一个衰减矩阵（门控矩阵）来统一表述：

状态矩阵中存储了所有历史信息，我们第望根据当前时刻输入从中获取最相关的，并且这个无限接近真实的状态矩阵可以理解成将作为训练语料训练得到的一个模型。我们的优化目标就是我们便用MSE作为损失函数，则：

应用梯度下降进行优化：

所以

把变成，则

为模型对的旧认知，为补充的新认知，除旧而迎新，这就是DeltaNet 在DeltaNet基础上添加门控：

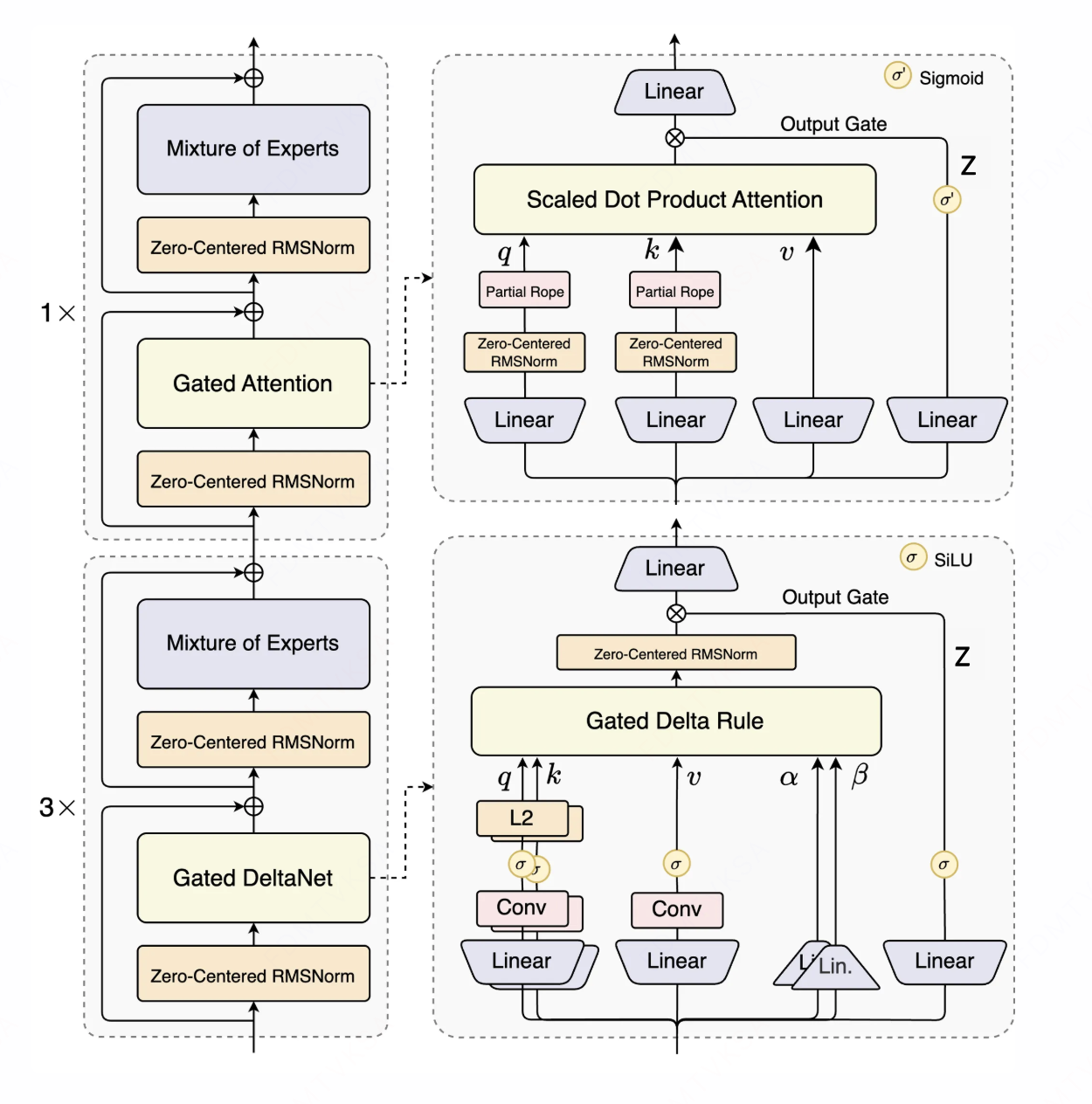
这就是Gated DeltaNet，也就是在qwen3－next模型中使用的线性注意力。苏神的博客中说只只乘到上会更好，即如下形式：

更加符合我们上面说的添加遗忘门的方式：

PS： 最初的线性Attention对应的损失函数为，即内积损失，优化模型预测的和真实的相似性，此时应用梯度下降进行优化：

即诙复了标准线性注意力更新。